• Microcontrolador; ATMega328
• 6 entradas analogicas (desde A0 hasta A5), que aceptan de 0 a 5V
• Pines de potencia: podemos alimentar un circuito con +5V, +3, 3V, conectar la masa GND, etc.
• Botón de reset: para reiniciar la placa.
• USB: para comunicarse con el ordenador.
• Alimentación externa: permite la alimentación mediante pilas o baterias dw entre 7 y 12 V para funcionar sin tener conectado el cable USB
  
  
  

2.- Define robot y pon 3 ejemplos de su uso en la actualidad.

Un robot es una máquina automática programable capaz de captar información de su entorno, procesarla y actuar en consecuencia

Ejemplo: en la actualidad se pueden utilizar para apagar incendios, detectar explosivos y para la agricultura.

Biografía Newton

Biografía:

Nació el 25 de Diciembre de 1642  en Woolsthorpe (Inglaterra) y murió el 23 de Marzo de 1727 en Kensington, siendo enterrado en el famoso convento de Westminster junto a los grandes de Inglaterra.

Su padre murió tres meses antes de que naciera y su madre se volvió a casar cuando Isaac apenas tenía tres años, por lo que fue criado por su abuela. Esta separación le traumatizó.

No fue un niño prodigio. Nació sietemesino en una familia de campesinos. Tuvo problemas de salud y dificultades en los estudios. Como era débil físicamente no jugaba con los niños de su edad, escribía poesías, dibujaba y construía juguetes.

Sus primeros estudios los realizó en las escuelas situadas en los pueblos cercanos a donde vivía, a las que iba andando. En estos colegios no era muy buen estudiante (era el penúltimo de la clase). Con 17 años le sacaron del colegio para ayudar a la granja familiar, pero se pasaba la mayor parte del tiempo resolviendo problemas, experimentando e ideando modelos mecánicos.

Como era un pésimo granjero, su madre y su tío decidieron que fuera al College Trinity de Cambridge donde ingresó en 1661 y se licenció en Artes en 1665. Pero ese mismo año se cerró la Universidad a causa de la peste y tuvo que volver a la granja.

Entre 1665 y 1667, estando en la granja (por culpa de la peste), concibió la mayor parte de las teorías que le han hecho famosos.

Regresó a Cambridge en 1667, primero como becario, luego como profesor y finalmente como catedrático.

En 1693, debido al exceso de trabajo (o a un autoenvenenamiento con uno de sus experimentos) se desplomó mentalmente. Derrumbe del que tardó meses en salir y desde entonces no fue el mismo genio que había sido hasta entonces.

En 1722 le aparecen cálculos renales y poco después empezó a tener problemas respiratorios, por lo que sus últimos años los pasó con bastantes dolores, aunque los acepto con resignación y dignidad. Murió a los 84 años.

Las tres leyes de Newton:

Primera ley o ley de inercia

La primera ley de Newton, conocida también como Ley de inercía, nos dice que si sobre un cuerpo no actua ningún otro, este permanecerá indefinidamente moviéndose en línea recta con velocidad constante (incluido el estado de reposo, que equivale a velocidad cero).

Como sabemos, el movimiento es relativo, es decir, depende de cual sea el observador que describa el movimiento. Así, para un pasajero de un tren, el supervisor viene caminando lentamente por el pasillo del tren, mientras que para alguien que ve pasar el tren desde el andén de una estación, el supervisor se está moviendo a una gran velocidad. Se necesita, por tanto, un sistema de referencia al cual referir el movimiento. La primera ley de Newton sirve para definir un tipo especial de sistemas de referencia conocidos como Sistemas de referencia inerciales, que son aquellos sistemas de referencia desde los que se observa que un cuerpo sobre el que no actúa ninguna fuerza neta se mueve con velocidad constante.

Segunda ley o Principio fundamental de la dinámica

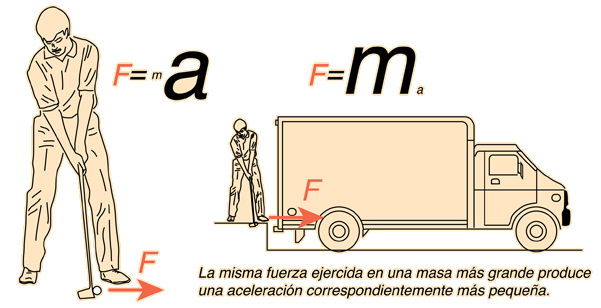
La aceleración de un objeto es directamente proporcional a la fuerza neta que actúa sobre el, tiene la dirección de la fuerza neta y es inversamente proporcional a la masa del objeto.

Esta ley nos dice que si un objeto está en movimiento, tiene una dirección, hacía cualquier lado.

Si resulta que el objeto ya se encontraba en movimiento, y si hay una fuerza que le agregue mas velocidad, el objeto aumentaría su rapidez.

         F= MxA 

  Tercera ley o principio de acción- reacción

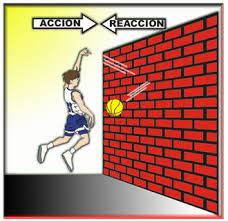
Siempre que un objeto ejerce una fuerza sobre un segundo objeto, el segundo objeto ejerce una fuerza de igual magnitud y dirección opuesta sobre el primero.

Esta ley nos dice que si un objeto golpea a otro objeto ambos objetos tienen la misma fuerza pero también tenemos que ver la masa del objeto en la que se está aplicando la fuerza y pueda ser que rebote el primer objeto que haya ejercido esa fuerza en el segundo objeto.

PROBLEMA DE LA PÁGINA 123: EN EL PARQUE DON JAVIER

PROBLEMA DE LA PÁGINA 123: En el parque don Javier

En esta entrada voy a hacer un problema del libro de la pagina 123

En el parque Don Javier se han localizado el mismo número de pájaros en el pino que en el chopo y, entre el pino, el chopo y la morera suman 111 pájaros.Si se cambiaran 8 pájaros del pino y otros 8 pájaros del chopo a anidar a la morera, los tres arboles tendrían el  mismo numero de pájaros.

1. Si se supone que hay x pájaros en el pino:

- Establece, en función de x, el número de pájaros que hay inicialmente en el chopo y en la morera



                                 CHOPO = X
                                 MORERA =111−2

   

El chopo tiene x ya que si suponemos que hay x pájaros en el pino y dice el problema que hay los mismos pájaros en los dos árboles pues decimos que el chopo es x. Y la morera es esa ecuación ya que si decimos que el chopo y el pino tiene x pájaros, pues decimos que es

111−2

ya que hay 111 pájaros en total y si restamos el doble de x ya que como hay dos árboles que tienen x. Esa es la ecuación que refleja los pájaros que hay en la morera.

- Utilizando esta incógnita, escribe el número de pájaros que habitaría en cada árbol después de la migración.

                    

                                             PINO =  x - 8

                                             CHOPO = x -8

MORERA = 111-2x +16

El pino y el chopo tendrían esos pájaros ya que si nos dice que los quitan 8 pájaros a cada uno de estos árboles y además si había los mismos pues utilizamos esa ecuación.
La morera tendría esos pájaros debido a que decimos que hay 111 en total que si les restamos el doble de x y luego les sumamos los 16 pájaros que se quitan de los otros dos árboles y con esa ecuación podríamos decir cuantos pájaros habrían en la morera después de la migración.
- Plantea y resuelve una ecuación para calcular cuántos pájaros vivían inicialmente en cada árbol. 

111=2x+(x−24)$$$$

111=2x+x−24

135=3x

1353=x

45=x$$$$

Había 45 pájaros en el pino y el chopo.

Ahora utilizando la ecuación que di antes para la morera:
45*2=90
Morera = 111-90
Morera = 21 pájaros

Había 21 pájaros en la morera. He sacado esta ecuación desde poder decir que el pino y el chopo tienen 2x pájaros. Luego el x-24 lo saco de que dice que la morera tendría todos los pájaros iguales si el pino y el chopo pierden 8 pájaros, por eso pongo x-24 ya que yo saco de esa aclaración que la diferencia del pino y el chopo con la morera es de 24 ya que si decimos que tiene x pájaros el chopo y el pino y los quitas 8 a cada uno que son 16 en total y se los sumas a la morera como habías restado antes 8 podríamos decir que la diferencia es de 24.

- El número de pájaros que hay en cada árbol después de la migración es:

                                            A=40
                                            B=39
                                            C=38
                                            D=37

Es 37 el número de pájaros ya que si multiplicas por 3 el 37 da 111 que es el total de pájaros y además si hacemos 45-8 es 37 y si hacemos 21+16 nos da 37. 

2. Si se supone que hay x pájaros en el pino y en el chopo e y en la morera: 

- Plantea y resuelve un sistema de ecuaciones para calcular cuántos pájaros vivían inicialmente en cada árbol:

2x+y=111

x−y=24

Estas son las dos ecuaciones que he hecho para poder resolver este sistema de ecuaciones, la primera es la ecuación que utilice antes y la segunda he cogido x que son los pájaros que hay en el pino o el chopo y los resto a y que, son los pájaros que hay en la morera, la diferencia sabemos que es 24 y esas son las dos ecuaciones que he utilizado.

Lo vamos a resolver por el sistema de REDUCCIÓN:

2x+x−y=111y=24

                                          y nos queda esto 

3x=135

x    =1353$$$$

                                     x=45

45−y=24

$$$$45−24=y

y=21$$$$

               Hay 45 pájaros en el pino y en el chopo y 21 en la morera. 

- Comprueba que las soluciones obtenidas concuerdan con el apartado 1:

Si concuerdan todas